地震の発生及びそれに伴う地震動の評価（地震ハザード評価）は、現状では数多くの不確定要素を含んでいる。現状の地震学・地震工学のレベルでは、将来発生する可能性のある地震について、地震発生の日時、場所、規模、発生する地震動等について、決定論的に1つの答えを準備することは困難である。こうした不確定性を定量的に評価するための技術的枠組みとして有力と考えられているのが、確率論的手法である。地震調査委員会が進めている地震動予測地図の作成においては、地震発生の不確定性及び強震動評価の不確定性を確率論的手法を用いて評価する試みがなされている。
確率論的地震動予測地図を作成するために、以下に述べる手法に従った地震ハザード評価が採用されている。地震ハザード評価とは、ある地点において将来発生する「地震動の強さ」、「対象とする期間」、「対象とする確率」の3つの関係を評価するものである。確率論的地震動予測地図作成における地震ハザード評価の大まかな手順は、以下に示す通りである。
このようにして、地点毎に地震ハザード評価を実施し、地震動の強さ・期間・確率のうち2つを固定して残る1つの値を求めた上で、それらの値の分布を示したものが「確率論的地震動予測地図」である。
具体的なハザード曲線の計算は、以下の手順に従って行う。着目地点において、その周辺で発生する地震（あるいは地震群）によって
年間に少なくとも1回地震動の強さが 
を超える確率 
を、一般にハザード曲線と呼ぶ。ハザード曲線は、地点の周辺で発生するいずれの地震（群）によっても
以下である確率を1から引くことにより、次式で評価される。
 |
(2.1.1) |
ここに、
は 
番目の地震（群）によって 年間に少なくとも1回地震動の強さが を超える確率であり、以下の(1)および(2)のように算定される。なお、以下の記述では、地震の規模と距離に関して離散的な表現としている。
(1) 震源を予め特定できる地震
これらの地震の発生確率は、過去の地震活動についてある程度の情報が得られている一部の地震については更新過程*あるいは時間予測モデルといった非定常な地震活動を表すモデルに基づき算定され、残りのものについては定常ポアソン過程を仮定して評価される。この場合、 番目の地震によって、地震動の強さが 年間に少なくとも1回 を超える確率 は、以下のようにして算定することができる。
a) 非定常な地震活動モデルに基づき地震発生確率が算定される場合
期間tの間に複数回の地震発生を考慮する場合、それぞれの地震時の地震動の強さが互いに独立であると仮定すると、地震動の強さが 年間に少なくとも1回 を超える確率 は、
 |
(2.1.2) |
で表される。ただし、
は期間 の間に 
回地震が発生する確率、 
は地震 が1度発生した条件下で地震動の強さが を超える条件付確率であり、
 |
(2.1.3) |
となる。ここに、
は 番目の地震における規模の確率関数、
は規模が 
の条件下での距離の確率関数、
は地震の規模が 、距離が 
の時に地震動の強さが 以上となる条件付確率である。距離減衰式を用いて地震動の強さを評価する場合には、
は距離減衰式の中央値 
とそのばらつき（中央値を1とする対数正規変量 
で表されることが多い）を用いて、
 |
(2.1.4) |
となる。ただし、
は の累積分布関数である。
なお、期間 に複数回の地震が発生する確率が無視できる場合には、式(2.1.2)は簡略化されて次式で表される。
 |
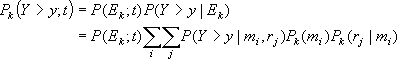(2.1.5) |
ただし、
は 番目の地震が 年間に発生する確率であり、更新過程あるいは時間予測モデルに基づき、BPT分布**を用いて評価される。
b) 地震の発生が定常ポアソン過程でモデル化される場合
地震の発生を定常ポアソン過程とした場合には、地震動の強さが 年間に を超える確率 は、
 |
(2.1.6) |
となる。ただし、
は 番目の地震によって地震動の強さが を超える年あたりの頻度であり、
 |
(2.1.7) |
となる。ここに、
は 番目の地震の年あたりの発生頻度、他はa)と同様である。
* 互いに重ならない時間区間における変動が互いに独立に同一の確率分布に従うようなものをいう。更新過程のうち、指数分布に従うものをポアソン過程という。
** BPTはBrownian Passage Time の略。１次元のブラウン運動において、ある状態に注目したとき、その状態に初めて達するまでにかかる時間をTとしたときに、Tが従う確率分布をいう。ここでは、ある地域で起こる一定の大きさ以上の地震の発生間隔にBPT分布を仮定している。BPT分布は、逆ガウス分布やワルド分布とも呼ばれている。
（２）震源断層を予め特定しにくい地震
上記（１）と異なり、対象とする地震を複数の規模と距離の組み合わせから成る群として取り扱う必要がある。これらの地震は、地域区分する方法と地域区分しない方法とを併用して評価するが、地域区分する方法の場合には地震活動域ごと、地域区分しない方法ではメッシュごとに、それぞれ地震活動が一様としている。地震の規模の確率分布は上限値を有するGutenberg-Richterの関係式から、また、距離の確率分布は地点と地震活動域あるいはメッシュとの幾何学的な位置関係からそれぞれ算定する。地震の発生時系列は、定常ポアソン過程でモデル化する。
以上から、グループ 
の地震によって、地震動の強さが 年間に を超える確率 
は、次式によって算定することができる。
 |
(2.1.8) |
ただし、
はグループ の地震によって地震動の強さが を超える年あたりの頻度であり、
 |
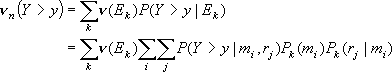(2.1.9) |
となる。ここに、 はグループ の地震を構成する 番目の地震活動域またはメッシュにおける最小マグニチュード（=5.0）以上の地震の年あたりの発生頻度、 はグループ の地震を構成する 番目の地震活動域またはメッシュで地震が1つ発生した場合に地点での地震動の強さが
を超える条件付確率、 は 番目の地震活動域またはメッシュにおける規模の確率関数、 は規模が の条件下での距離の確率関数、 は地震の規模がが 、距離が の時に地震動の強さが を超える条件付確率である。
なお、震源断層を予め特定しにくい地震では、上述のように、地震の規模の確率分布を、Gutenberg-Richter式に従うモデル（いわゆる
値モデル）でモデル化している。厳密には、領域ごとに最大マグニチュードを設定しているため、上限値を有する
値モデル（truncated 値モデル）となっている。マグニチュードの上限値（と下限値）を有する 値モデルでは、
 |
(2.1.10) | |
 |
(2.1.11) |
と、Gutenberg-Richter式
 |
(2.1.12) |
より、マグニチュード 
の分布関数は、
 |
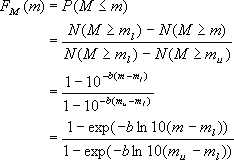(2.1.13) |
となる。ここで、
と 
は最小と最大のマグニチュードであるが、一般にはマグニチュードの刻み 
は0.1とすることが多く、この場合には、（0.1刻みで表示された）最小マグニチュードが5.0の場合、 には5.0− /2=4.95が、同様に には0.1刻みの最大マグニチュード＋ /2が用いられる。上記の式(2.1.13)を用いて、マグニチュード が となる確率は、
として、
 |
(2.1.14) |
となる。最大値を設定しない 値モデルでは、規模別の累積発生頻度が片対数軸上で直線となるが、上限値が設定されている場合には、規模別の累積発生頻度は直線にはならないことに注意が必要である。
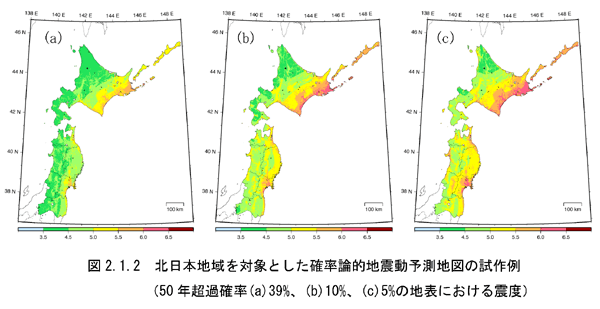
現在作成中の全国を概観した確率論的地震動予測地図では、日本全国を約1kmメッシュに分割し、工学的基盤（S波速度400m/s）での最大速度、地表での最大速度、及び最大速度から変換した計測震度の計算を行っている。確率論的地震動予測地図作成のためには、将来発生する可能性のある全ての地震について、その発生確率及び地震が発生したときの強震動評価を、不確定性を考慮して行う必要がある。そのため、後述するシナリオ地震に対する強震動評価で用いる詳細な計算手法は、計算作業が膨大なものとなり、事実上採用することが不可能である。確率論的地震動予測地図の作成では、簡便な強震動評価手法として、経験的距離減衰式1)が用いられている。図2.1.2に地震調査委員会より公表された北日本地域を対象とした確率論的地震動予測地図の試作例2)を示す。なお、作成手法の詳細な説明については防災科学技術研究所研究資料3)を参照頂きたい。
|
|
|
| ← Back | Next → |